Uniform 5-polytope
In geometry, a uniform polyteron[1][2] (or uniform 5-polytope) is a five-dimensional uniform polytope. By definition, a uniform polyteron is vertex-transitive and constructed from uniform polychoron facets.
The complete set of convex uniform polytera has not been determined, but most can be made as Wythoff constructions from a small set of symmetry groups. These construction operations are represented by the permutations of rings of the Coxeter-Dynkin diagrams.
Contents |
Regular 5-polytopes
Regular 5-polytopes can be represented by the Schläfli symbol {p,q,r,s}, with s {p,q,r} polychoral facets around each face. There are exactly three such regular polytopes, all convex:
- {3,3,3,3} - Hexateron (5-simplex)
- {4,3,3,3} - Penteract (5-hypercube)
- {3,3,3,4} - Pentacross (5-orthoplex)
There are no nonconvex regular polytopes in 5 or more dimensions.
Convex uniform 5-polytopes
There are 105 known convex uniform 5-polytopes, plus a number of infinite families of duoprism prisms, and polygon-polyhedron duoprisms. All except the grand antiprism prism are based on Wythoff constructions, reflection symmetry generated with Coxeter groups.
Reflection families
The hexateron is the regular form in the A5 family. The penteract and pentacross are the regular forms in the B5 family. The bifurcating graph of the D6 family contains the pentacross, as well as a demipenteract which is an alternated penteract.
Fundamental families
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | A5 | [34] | |
| 2 | B5 | [4,33] | |
| 3 | D5 | [32,1,1] | |
Uniform prisms There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes:
| # | Coxeter groups | Coxeter graph | |
|---|---|---|---|
| 1 | A4 × A1 | [3,3,3] × [ ] | |
| 2 | B4 × A1 | [4,3,3] × [ ] | |
| 3 | F4 × A1 | [3,4,3] × [ ] | |
| 4 | H4 × A1 | [5,3,3] × [ ] | |
| 5 | D4 × A1 | [31,1,1] × [ ] | |
There is one infinite family of 5-polytopes based on prisms of the uniform duoprisms {p}×{q}×{ }:
| Coxeter groups | Coxeter graph | |
|---|---|---|
| I2(p) × I2(q) × A1 | [p] × [q] × [ ] | |
Uniform duoprisms
There are 3 categorical uniform duoprismatic families of polytopes based on Cartesian products of the uniform polyhedra and regular polygons: {q,r}×{p}:
| # | Coxeter groups | Coxeter graph | |
|---|---|---|---|
| 1 | A3 × I2(p) | [3,3] × [p] | |
| 2 | B3 × I2(p) | [4,3] × [p] | |
| 3. | H3 × I2(p) | [5,3] × [p] | |
Enumerating the convex uniform 5-polytopes
- Simplex family: A5 [34]
- 19 uniform 5-polytopes
- Hypercube/Orthoplex family: BC5 [4,33]
- 31 uniform 5-polytopes
- Demihypercube D5/E5 family: [32,1,1]
- 23 uniform 5-polytopes (8 unique)
- Prisms and duoprisms:
- 56 uniform 5-polytope (46 unique) constructions based on prismatic families: [3,3,3]x[ ], [4,3,3]x[ ], [5,3,3]x[ ], [31,1,1]x[ ].
- One non-Wythoffian - The grand antiprism prism is the only known non-Wythoffian convex uniform 5-polytope, constructed from two grand antiprisms connected by polyhedral prisms.
That brings the tally to: 19+31+8+46+1=105
In addition there are:
- Infinitely many uniform 5-polytope constructions based on duoprism prismatic families: [p]x[q]x[ ].
- Infinitely many uniform 5-polytope constructions based on duoprismatic families: [3,3]x[p], [4,3]x[p], [5,3]x[p].
The A5 family
There are 19 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. (16+4-1 cases)
They are named by Norman Johnson from the Wythoff construction operations upon regular 5-simplex (hexateron).
The A5 family has symmetry of order 720 (6 factorial).
The coordinates of uniform 5-polytopes with 5-simplex symmetry can be generated as permutations of simple integers in 6-space, all in hyperplanes with normal vector (1,1,1,1,1,1).
See symmetry graphs: List of A5 polytopes
| # | Base point | Johnson naming system Bowers name and (acronym) Coxeter-Dynkin |
k-face element counts | Vertex figure |
Facet counts by location: [3,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [3,3,3] (6) |
[3,3]×[ ] (15) |
[3]×[3] (20) |
[ ]×[3,3] (15) |
[3,3,3] (6) |
||||
| 1 | (0,0,0,0,0,1) or (0,1,1,1,1,1) | 5-simplex hexateron (hix) |
6 | 15 | 20 | 15 | 6 | {3,3,3} |
(5) {3,3,3} |
- | - | - | - |
| 2 | (0,0,0,0,1,1) or (0,0,1,1,1,1) | Rectified 5-simplex rectified hexateron (rix) |
12 | 45 | 80 | 60 | 15 | t{3,3}x{ } |
(4) t1{3,3,3} |
- | - | - | (2) {3,3,3} |
| 3 | (0,0,0,0,1,2) or (0,1,2,2,2,2) | Truncated 5-simplex truncated hexateron (tix) |
12 | 60 | 120 | 90 | 20 | Tetrah.pyr |
(4) t0,1{3,3,3} |
- | - | - | (1) {3,3,3} |
| 4 | (0,0,0,1,1,1) | Birectified 5-simplex dodecateron (dot) |
12 | 45 | 80 | 75 | 30 | {3}x{3} |
(3) t1{3,3,3} |
- | - | - | (3) t1{3,3,3} |
| 5 | (0,0,0,1,1,2) or (0,1,1,2,2,2) | Cantellated 5-simplex small rhombated hexateron (sarx) |
12 | 60 | 140 | 150 | 60 | prism-wedge |
(3) t0,2{3,3,3} |
- | - | (1) × { }×{3,3} |
(1) t1{3,3,3} |
| 6 | (0,0,0,1,2,2) or (0,0,1,2,2,2) | Bitruncated 5-simplex bitruncated hexateron (bittix) |
27 | 135 | 290 | 240 | 60 | (3) t1,2{3,3,3} |
- | - | - | (2) t0,1{3,3,3} |
|
| 7 | (0,0,0,1,2,3) or (0,1,2,3,3,3) | Cantitruncated 5-simplex great rhombated hexateron (garx) |
32 | 180 | 420 | 360 | 90 | t0,1,2{3,3,3} |
- | - | × { }×{3,3} |
t0,1{3,3,3} |
|
| 8 | (0,0,1,1,1,2) or (0,1,1,1,2,2) | Runcinated 5-simplex small prismated hexateron (spix) |
47 | 255 | 420 | 270 | 60 | (2) t0,3{3,3,3} |
- | (3) × {3}×{3} |
(3) × { }×t1{3,3} |
(1) t1{3,3,3} |
|
| 9 | (0,0,1,1,2,2) | Bicantellated 5-simplex small birhombated dodecateron (sibrid) |
62 | 180 | 210 | 120 | 30 | (2) t0,2{3,3,3} |
- | (8) × {3}×{3} |
- | (2) t0,2{3,3,3} |
|
| 10 | (0,0,1,1,2,3) or (0,1,2,2,3,3) | Runcitruncated 5-simplex prismatotruncated hexateron (pattix) |
27 | 135 | 290 | 300 | 120 | t0,1,3{3,3,3} |
- | × {6}×{3} |
× { }×t1{3,3} |
t0,2{3,3,3} |
|
| 11 | (0,0,1,2,2,3) or (0,1,1,2,3,3) | Runcicantellated 5-simplex prismatorhombated hexateron (pirx) |
32 | 180 | 420 | 450 | 180 | t0,1,3{3,3,3} |
- | × {3}×{3} |
× { }×t0,1{3,3} |
t1,2{3,3,3} |
|
| 12 | (0,0,1,2,3,3) | Bicantitruncated 5-simplex great birhombated dodecateron (gibrid) |
47 | 315 | 720 | 630 | 180 | t0,1,2{3,3,3} |
- | × {3}×{3} |
- | t0,1,2{3,3,3} |
|
| 13 | (0,0,1,2,3,4) or (0,1,2,3,4,4) | Runcicantitruncated 5-simplex great prismated hexateron (gippix) |
47 | 255 | 570 | 540 | 180 | Irr.5-cell |
t0,1,2,3{3,3,3} |
- | × {3}×{6} |
× { }×t0,1{3,3} |
t0,2{3,3,3} |
| 14 | (0,1,1,1,1,2) | Stericated 5-simplex small cellated dodecateron (scad) |
62 | 330 | 570 | 420 | 120 | Irr.16-cell |
(1) {3,3,3} |
(4) × { }×{3,3} |
(6) × {3}×{3} |
(4) × { }×{3,3} |
(1) {3,3,3} |
| 15 | (0,1,1,1,2,3) or (0,1,2,2,2,3) | Steritruncated 5-simplex celliprismated hexateron (cappix) |
62 | 420 | 900 | 720 | 180 | t0,1{3,3,3} |
× { }×t0,1{3,3} |
× {3}×{6} |
× { }×{3,3} |
t0,3{3,3,3} |
|
| 16 | (0,1,1,2,2,3) | Stericantellated 5-simplex small cellirhombated dodecateron (card) |
47 | 315 | 810 | 900 | 360 | t0,2{3,3,3} |
× { }×t0,2{3,3} |
× {3}×{3} |
× { }×t0,2{3,3} |
t0,2{3,3,3} |
|
| 17 | (0,1,1,2,3,4) or (0,1,2,3,3,4) | Stericantitruncated 5-simplex celligreatorhombated hexateron (cograx) |
62 | 480 | 1140 | 1080 | 360 | t0,1,2{3,3,3} |
× { }×t0,1,2{3,3} |
× {3}×{6} |
× { }×t0,2{3,3} |
t0,1,3{3,3,3} |
|
| 18 | (0,1,2,2,3,4) | Steriruncitruncated 5-simplex celliprismatotruncated dodecateron (captid) |
62 | 450 | 1110 | 1080 | 360 | t0,1,3{3,3,3} |
× { }×t0,1{3,3} |
× {6}×{6} |
× { }×t0,1,3{3,3} |
t0,1,3{3,3,3} |
|
| 19 | (0,1,2,3,4,5) | Omnitruncated 5-simplex great cellated dodecateron (gocad) |
62 | 540 | 1560 | 1800 | 720 | Irr. {3,3,3} |
(1) t0,1,2,3{3,3,3} |
(1) × { }×t0,1,2{3,3} |
(1) × {6}×{6} |
(1) × { }×t0,1,2{3,3} |
(1) t0,1,2,3{3,3,3} |
The B5 family
The B5 family has symmetry of order 3840 (5!×25).
This family has 25−1=31 Wythoffian uniform polytopes generated by marking one or more nodes of the Coxeter-Dynkin diagram.
For simplicity it is divided into two subgroups, each with 12 forms, and 7 "middle" forms which equally belong in both.
The penteractic family of polytera are given by the convex hulls of the base points listed in the following table, with all permutations of coordinates and sign taken. Each base point generates a distinct uniform polyteron. All coordinates correspond with uniform polytera of edge length 2.
See symmetry graph: List of B5 polytopes
| # | Base point | Name Coxeter-Dynkin |
Element counts | Vertex figure |
Facet counts by location: [4,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [4,3,3] (10) |
[4,3]×[ ] (40) |
[4]×[3] (80) |
[ ]×[3,3] (80) |
[3,3,3] (32) |
||||
| 1 | (0,0,0,0,1)√2 | 5-orthoplex (Quadrirectified 5-cube) |
10 | 40 | 80 | 80 | 32 | {3,3,4} |
{3,3,3} |
- | - | - | - |
| 2 | (0,0,0,1,1)√2 | Rectified 5-orthoplex (Trirectified 5-cube) |
42 | 200 | 400 | 320 | 80 | { }×{3,4} |
{3,3,4} |
- | - | - | t1{3,3,3} |
| 3 | (0,0,0,1,2)√2 | Truncated 5-orthoplex (Quadritruncated 5-cube) |
42 | 200 | 400 | 400 | 160 | (Octah.pyr) |
t0,1{3,3,3} |
{3,3,3} |
- | - | - |
| 4 | (0,0,1,1,1)√2 | Birectified 5-cube (Birectified 5-orthoplex) |
42 | 280 | 640 | 480 | 80 | {4}×{3} |
t1{3,3,4} |
- | - | - | t1{3,3,3} |
| 5 | (0,0,1,1,2)√2 | Cantellated 5-orthoplex (Tricantellated 5-cube) |
122 | 680 | 1520 | 1280 | 320 | Prism-wedge |
t1{3,3,4} | { }×{3,4} | - | - | t0,2{3,3,3} |
| 6 | (0,0,1,2,2)√2 | Bitruncated 5-orthoplex (tritruncated 5-cube) |
42 | 280 | 720 | 800 | 320 | t0,1{3,3,4} | - | - | - | t1,2{3,3,3} |
|
| 7 | (0,0,1,2,3)√2 | Cantitruncated 5-orthoplex (tricantitruncated 5-orthoplex) |
122 | 680 | 1520 | 1600 | 640 | t0,2{3,3,4} | { }×t1{3,4} | {6}×{4} |
- | t0,1,3{3,3,3} |
|
| 8 | (0,1,1,1,1)√2 | Rectified 5-cube |
42 | 240 | 400 | 240 | 40 | {3,3}x{ } |
t1{4,3,3} |
- | - | - | {3,3,3} |
| 9 | (0,1,1,1,2)√2 | Runcinated 5-orthoplex |
202 | 1240 | 2160 | 1440 | 320 | t1{4,3,3} | - | {3}×{4} |
t0,3{3,3,3} |
||
| 10 | (0,1,1,2,2)√2 | Bicantellated 5-cube (Bicantellated 5-orthoplex) |
122 | 840 | 2160 | 1920 | 480 | t0,2{4,3,3} |
- | {4}×{3} |
- | t0,2{3,3,3} |
|
| 11 | (0,1,1,2,3)√2 | Runcitruncated 5-orthoplex |
202 | 1560 | 3760 | 3360 | 960 | t0,2{3,3,4} | { }×t1{3,4} | {6}×{4} |
- | t0,1,3{3,3,3} |
|
| 12 | (0,1,2,2,2)√2 | Bitruncated 5-cube |
42 | 280 | 720 | 720 | 240 | t1,2{4,3,3} |
- | - | - | t0,1{3,3,3} |
|
| 13 | (0,1,2,2,3)√2 | Runcicantellated 5-orthoplex |
202 | 1240 | 2960 | 2880 | 960 | { }×t0,1{3,4} | t1,2{3,3,4} | {3}×{4} |
- | t0,1,3{3,3,3} |
|
| 14 | (0,1,2,3,3)√2 | Bicantitruncated 5-cube (Bicantitruncated 5-orthoplex) |
122 | 840 | 2160 | 2400 | 960 | t0,2{4,3,3} |
- | {4}×{3} |
- | t0,2{3,3,3} |
|
| 15 | (0,1,2,3,4)√2 | Runcicantitruncated 5-orthoplex |
202 | 1560 | 4240 | 4800 | 1920 | t0,1,2{3,3,4} | { }×t0,1{3,4} | {6}×{4} |
- | t0,1,2,3{3,3,3} |
|
| 16 | (1,1,1,1,1) | 5-cube |
32 | 80 | 80 | 40 | 10 | {3,3,3} |
{4,3,3} |
- | - | - | - |
| 17 | (1,1,1,1,1) + (0,0,0,0,1)√2 |
Stericated 5-cube (Stericated 5-orthoplex) |
242 | 800 | 1040 | 640 | 160 | Tetr.antiprm |
{4,3,3} |
{4,3}×{ } |
{4}×{3} |
{ }×{3,3} |
{3,3,3} |
| 18 | (1,1,1,1,1) + (0,0,0,1,1)√2 |
Runcinated 5-cube |
162 | 1200 | 2160 | 1440 | 320 | t0,3{4,3,3} |
- | {4}×{3} |
{ }×t1{3,3} |
{3,3,3} |
|
| 19 | (1,1,1,1,1) + (0,0,0,1,2)√2 |
Steritruncated 5-orthoplex |
242 | 1600 | 2960 | 2240 | 640 | t0,3{3,3,4} | { }×{4,3} | - | - | t0,1{3,3,3} |
|
| 20 | (1,1,1,1,1) + (0,0,1,1,1)√2 |
Cantellated 5-cube |
82 | 640 | 1520 | 1200 | 240 | Prism-wedge |
t0,2{4,3,3} |
- | - | { }×{3,3} |
t1{3,3,3} |
| 21 | (1,1,1,1,1) + (0,0,1,1,2)√2 |
Stericantellated 5-cube (Stericantellated 5-orthoplex) |
242 | 2080 | 4720 | 3840 | 960 | t0,2{4,3,3} |
t0,2{4,3}×{ } |
{4}×{3} |
{ }×t0,2{3,3} |
t0,2{3,3,3} |
|
| 22 | (1,1,1,1,1) + (0,0,1,2,2)√2 |
Runcicantellated 5-cube |
162 | 1200 | 2960 | 2880 | 960 | t0,1,3{4,3,3} |
- | {4}×{3} |
{ }×t0,1{3,3} |
t1,2{3,3,3} |
|
| 23 | (1,1,1,1,1) + (0,0,1,2,3)√2 |
Stericantitruncated 5-orthoplex |
242 | 2400 | 6000 | 5760 | 1920 | { }×t0,2{3,4} |
t0,1,3{3,3,4} |
{6}×{4} |
{ }×t0,1{3,3} |
t0,1,2{3,3,3} |
|
| 24 | (1,1,1,1,1) + (0,1,1,1,1)√2 |
Truncated 5-cube |
42 | 240 | 400 | 280 | 80 | Tetrah.pyr |
t0,1{4,3,3} |
- | - | - | {3,3,3} |
| 25 | (1,1,1,1,1) + (0,1,1,1,2)√2 |
Steritruncated 5-cube |
242 | 1520 | 2880 | 2240 | 640 | t0,1{4,3,3} |
t0,1{4,3}×{ } |
{8}×{3} |
{ }×{3,3} |
t0,3{3,3,3} |
|
| 26 | (1,1,1,1,1) + (0,1,1,2,2)√2 |
Runcitruncated 5-cube |
162 | 1440 | 3680 | 3360 | 960 | t0,1,3{4,3,3} |
{ }×t0,1{4,3} | {6}×{8} |
{ }×t0,1{3,3} | t0,1,3{3,3,3}]] | |
| 27 | (1,1,1,1,1) + (0,1,1,2,3)√2 |
Steriruncitruncated 5-cube (Steriruncitruncated 5-orthoplex) |
242 | 2160 | 5760 | 5760 | 1920 | t0,1,3{4,3,3} |
t0,1{4,3}×{ } |
{8}×{6} |
{ }×t0,1{3,3} |
t0,1,3{3,3,3} |
|
| 28 | (1,1,1,1,1) + (0,1,2,2,2)√2 |
cantitruncated 5-cube |
82 | 640 | 1520 | 1440 | 480 | t0,1,2{4,3,3} |
- | - | { }×{3,3} |
t0,1{3,3,3} |
|
| 29 | (1,1,1,1,1) + (0,1,2,2,3)√2 |
Stericantitruncated 5-cube |
242 | 2320 | 5920 | 5760 | 1920 | t0,1,2{4,3,3} |
t0,1,2{4,3}×{ } |
{8}×{3} |
{ }×t0,2{3,3} |
t0,1,3{3,3,3} |
|
| 30 | (1,1,1,1,1) + (0,1,2,3,3)√2 |
Runcicantitruncated 5-cube |
162 | 1440 | 4160 | 4800 | 1920 | t0,1,2,3{4,3,3} |
- | {8}×{3} |
{ }×t0,1{3,3} |
t0,1,2{3,3,3} |
|
| 31 | (1,1,1,1,1) + (0,1,2,3,4)√2 |
Omnitruncated 5-cube (omnitruncated 5-orthoplex) |
242 | 2640 | 8160 | 9600 | 3840 | Irr. {3,3,3} |
t0,1,2{4,3}×{ } |
t0,1,2{4,3}×{ } |
{8}×{6} |
{ }×t0,1,2{3,3} |
t0,1,2,3{3,3,3} |
The D5 family
The D5 family has symmetry of order 1920 (5! x 24).
This family has 23 Wythoffian uniform polyhedra, from 3x8-1 permutations of the D5 Coxeter-Dynkin diagram with one or more rings. 15 (2x8-1) are repeated from the B5 family and 8 are unique to this family.
See symmetry graphs: List of D5 polytopes
| # | Coxeter-Dynkin diagram Schläfli symbol symbols Johnson and Bowers names |
Element counts | Vertex figure |
Facets by location: [31,2,1] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [3,3,3] (16) |
[31,1,1] (10) |
[3,3]×[ ] (40) |
[ ]×[3]×[ ] (80) |
[3,3,3] (16) |
|||
| 51 | (121) 5-demicube Hemipenteract (hin) |
26 | 120 | 160 | 80 | 16 | t1{3,3,3} |
{3,3,3} | t0(111) | - | - | - |
| 52 | t0,1(121) Truncated 5-demicube Truncated hemipenteract (thin) |
42 | 280 | 640 | 560 | 160 | ||||||
| 53 | t0,2(121) Cantellated 5-demicube Small rhombated hemipenteract (sirhin) |
42 | 360 | 880 | 720 | 160 | ||||||
| 54 | t0,3(121) Runcinated 5-demicube Small prismated hemipenteract (siphin) |
82 | 480 | 720 | 400 | 80 | ||||||
| 55 | t0,1,2(121) Cantitruncated 5-demicube Great rhombated hemipenteract (girhin) |
42 | 360 | 1040 | 1200 | 480 | ||||||
| 56 | t0,1,3(121) Runcitruncated 5-demicube Prismatotruncated hemipenteract (pithin) |
82 | 720 | 1840 | 1680 | 480 | ||||||
| 57 | t0,2,3(121) Runcicantellated 5-demicube Prismatorhombated hemipenteract (pirhin) |
82 | 560 | 1280 | 1120 | 320 | ||||||
| 58 | t0,1,2,3(121) Runcicantitruncated 5-demicube Great prismated hemipenteract (giphin) |
82 | 720 | 2080 | 2400 | 960 | ||||||
Uniform prismatic forms
There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes:
A4 × A1
This prismatic family has 9 forms:
The A1 x A4 family has symmetry of order 240 (2*5!).
| # | Coxeter-Dynkin and Schläfli symbols Name |
Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 59 | {3,3,3}x{ } 5-cell prism |
7 | 20 | 30 | 25 | 10 |
| 60 | t1{3,3,3}x{ } Rectified 5-cell prism |
12 | 50 | 90 | 70 | 20 |
| 61 | t0,1{3,3,3}x{ } Truncated 5-cell prism |
12 | 50 | 100 | 100 | 40 |
| 62 | t0,2{3,3,3}x{ } Cantellated 5-cell prism |
22 | 120 | 250 | 210 | 60 |
| 63 | t0,3{3,3,3}x{ } Runcinated 5-cell prism |
32 | 130 | 200 | 140 | 40 |
| 64 | t1,2{3,3,3}x{ } Bitruncated 5-cell prism |
12 | 60 | 140 | 150 | 60 |
| 65 | t0,1,2{3,3,3}x{ } Cantitruncated 5-cell prism |
22 | 120 | 280 | 300 | 120 |
| 66 | t0,1,3{3,3,3}x{ } Runcitruncated 5-cell prism |
32 | 180 | 390 | 360 | 120 |
| 67 | t0,1,2,3{3,3,3}x{ } Omnitruncated 5-cell prism |
32 | 210 | 540 | 600 | 240 |
B4 × A1
This prismatic family has 16 forms. (Three are shared with [3,4,3]×[ ] family)
The A1 x B4 family has symmetry of order 768 (2*2^4*4!).
| # | Coxeter-Dynkin and Schläfli symbols Name |
Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 68 | {4,3,3}x{ } Tesseractic prism |
10 | 40 | 80 | 80 | 32 |
| 69 | t1{4,3,3}x{ } Rectified tesseractic prism |
26 | 136 | 272 | 224 | 64 |
| 70 | t0,1{4,3,3}x{ } Truncated tesseractic prism |
26 | 136 | 304 | 320 | 128 |
| 71 | t0,2{4,3,3}x{ } Cantellated tesseractic prism |
58 | 360 | 784 | 672 | 192 |
| 72 | t0,3{4,3,3}x{ } Runcinated tesseractic prism |
82 | 368 | 608 | 448 | 128 |
| 73 | t1,2{4,3,3}x{ } Bitruncated tesseractic prism |
26 | 168 | 432 | 480 | 192 |
| 74 | t0,1,2{4,3,3}x{ } Cantitruncated tesseractic prism |
58 | 360 | 880 | 960 | 384 |
| 75 | t0,1,3{4,3,3}x{ } Runcitruncated tesseractic prism |
82 | 528 | 1216 | 1152 | 384 |
| 76 | t0,1,2,3{4,3,3}x{ } Omnitruncated tesseractic prism |
82 | 624 | 1696 | 1920 | 768 |
| 77 | {3,3,4}x{ } 16-cell prism |
18 | 64 | 88 | 56 | 16 |
| 78 | t1{3,3,4}x{ } Rectified 16-cell prism (Same as 24-cell prism) |
26 | 144 | 288 | 216 | 48 |
| 79 | t0,1{3,3,4}x{ } Truncated 16-cell prism |
26 | 144 | 312 | 288 | 96 |
| 80 | t0,2{3,3,4}x{ } Cantellated 16-cell prism (Same as rectified 24-cell prism) |
50 | 336 | 768 | 672 | 192 |
| 81 | t0,1,2{3,3,4}x{ } Cantitruncated 16-cell prism (Same as truncated 24-cell prism) |
50 | 336 | 864 | 960 | 384 |
| 82 | t0,1,3{3,3,4}x{ } Runcitruncated 16-cell prism |
82 | 528 | 1216 | 1152 | 384 |
F4 × A1
This prismatic family has 10 forms.
The A1 x F4 family has symmetry of order 2304 (2*1152).
| # | Coxeter-Dynkin and Schläfli symbols Name |
Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| [79] | {3,4,3}x{ } 24-cell prism |
26 | 144 | 288 | 216 | 48 |
| [80] | t1{3,4,3}x{ } rectified 24-cell prism |
50 | 336 | 768 | 672 | 192 |
| [81] | t0,1{3,4,3}x{ } truncated 24-cell prism |
50 | 336 | 864 | 960 | 384 |
| 84 | t0,2{3,4,3}x{ } cantellated 24-cell prism |
146 | 1008 | 2304 | 2016 | 576 |
| 85 | t0,3{3,4,3}x{ } runcinated 24-cell prism |
242 | 1152 | 1920 | 1296 | 288 |
| 86 | t1,2{3,4,3}x{ } bitruncated 24-cell prism |
50 | 432 | 1248 | 1440 | 576 |
| 87 | t0,1,2{3,4,3}x{ } cantitruncated 24-cell prism |
146 | 1008 | 2592 | 2880 | 1152 |
| 88 | t0,1,3{3,4,3}x{ } runcitruncated 24-cell prism |
242 | 1584 | 3648 | 3456 | 1152 |
| 89 | t0,1,2,3{3,4,3}x{ } omnitruncated 24-cell prism |
242 | 1872 | 5088 | 5760 | 2304 |
| [83] | h0,1{3,4,3}x{ } snub 24-cell prism |
146 | 768 | 1392 | 960 | 192 |
H4 × A1
This prismatic family has 15 forms:
The A1 x H4 family has symmetry of order 28800 (2*14400).
| # | Coxeter-Dynkin and Schläfli symbols Name |
Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 90 | {5,3,3}x{ } 120-cell prism |
122 | 960 | 2640 | 3000 | 1200 |
| 91 | t1{5,3,3}x{ } Rectified 120-cell prism |
722 | 4560 | 9840 | 8400 | 2400 |
| 92 | t0,1{5,3,3}x{ } Truncated 120-cell prism |
722 | 4560 | 11040 | 12000 | 4800 |
| 93 | t0,2{5,3,3}x{ } Cantellated 120-cell prism |
1922 | 12960 | 29040 | 25200 | 7200 |
| 94 | t0,3{5,3,3}x{ } Runcinated 120-cell prism |
2642 | 12720 | 22080 | 16800 | 4800 |
| 95 | t1,2{5,3,3}x{ } Bitruncated 120-cell prism |
722 | 5760 | 15840 | 18000 | 7200 |
| 96 | t0,1,2{5,3,3}x{ } Cantitruncated 120-cell prism |
1922 | 12960 | 32640 | 36000 | 14400 |
| 97 | t0,1,3{5,3,3}x{ } Runcitruncated 120-cell prism |
2642 | 18720 | 44880 | 43200 | 14400 |
| 98 | t0,1,2,3{5,3,3}x{ } Omnitruncated 120-cell prism |
2642 | 22320 | 62880 | 72000 | 28800 |
| 99 | {3,3,5}x{ } 600-cell prism |
602 | 2400 | 3120 | 1560 | 240 |
| 100 | t1{3,3,5}x{ } Rectified 600-cell prism |
722 | 5040 | 10800 | 7920 | 1440 |
| 101 | t0,1{3,3,5}x{ } Truncated 600-cell prism |
722 | 5040 | 11520 | 10080 | 2880 |
| 102 | t0,2{3,3,5}x{ } Cantellated 600-cell prism |
1442 | 11520 | 28080 | 25200 | 7200 |
| 103 | t0,1,2{3,3,5}x{ } Cantitruncated 600-cell prism |
1442 | 11520 | 31680 | 36000 | 14400 |
| 104 | t0,1,3{3,3,5}x{ } Runcitruncated 600-cell prism |
2642 | 18720 | 44880 | 43200 | 14400 |
Grand antiprism prism
The grand antiprism prism is the only known convex nonwythoffian uniform polyteron. It has 200 vertices, 1100 edges, 1940 faces (40 pentagons, 500 squares, 1400 triangles), 1360 cells (300 tetrahedrons, 20 pentagonal antiprisms, 700 triangular prisms, 20 pentagonal prisms), 322 hypercells (2 grand antiprisms , 20 pentagonal antiprism prisms , and 300 tetrahedral prisms ).
| # | Name | Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 105 | grand antiprism prism Gappip |
322 | 1360 | 1940 | 1100 | 200 |
Notes on the Wythoff construction for the uniform 5-polytopes
Construction of the reflective 5-dimensional uniform polytopes are done through a Wythoff construction process, and represented through a Coxeter-Dynkin diagram, where each node represents a mirror. Nodes are ringed to imply which mirrors are active. The full set of uniform polytopes generated are based on the unique permutations of ringed nodes. Uniform 5-polytopes are named in relation to the regular polytopes in each family. Some families have two regular constructors and thus may have two ways of naming them.
Here's the primary operators available for constructing and naming the uniform 5-polytopes.
The last operation, the snub, and more generally the alternation, are the operation that can create nonreflective forms. These are drawn with "hollow rings" at the nodes.
The prismatic forms and bifurcating graphs can use the same truncation indexing notation, but require an explicit numbering system on the nodes for clarity.
| Operation | Extended Schläfli symbol |
Coxeter- Dynkin diagram |
Description |
|---|---|---|---|
| Parent | t0{p,q,r,s} | Any regular 5-polytope | |
| Rectified | t1{p,q,r,s} | The edges are fully truncated into single points. The 5-polytope now has the combined faces of the parent and dual. | |
| Birectified | t2{p,q,r,s} | Birectification reduces cells to their duals. | |
| Truncated | t0,1{p,q,r,s} | Each original vertex is cut off, with a new face filling the gap. Truncation has a degree of freedom, which has one solution that creates a uniform truncated 5-polytope. The 5-polytope has its original faces doubled in sides, and contains the faces of the dual. |
|
| Cantellated | t0,2{p,q,r,s} | In addition to vertex truncation, each original edge is beveled with new rectangular faces appearing in their place. A uniform cantellation is half way between both the parent and dual forms. |
|
| Runcinated | t0,3{p,q,r,s} | Runcination reduces cells and creates new cells at the vertices and edges. | |
| Stericated | t0,4{p,q,r,s} | Sterication reduces facets and creates new facets (hypercells) at the vertices and edges in the gaps. (Same as expansion operation for polyterons.) | |
| Omnitruncated | t0,1,2,3,4{p,q,r,s} | All four operators, truncation, cantellation, runcination, and sterication are applied. |
Regular and uniform honeycombs
There are five fundamental affine Coxeter groups, and 13 prismatic groups that generate regular and uniform tessellations in Euclidean 4-space.[3]
| # | Coxeter group | Coxeter-Dynkin diagram | ||
|---|---|---|---|---|
| 1 | 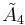 |
[3[5]] | [(3,3,3,3,3)] | |
| 2 | 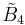 |
[4,3,31,1] | ||
| 3 | 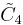 |
[4,3,3,4] | h[4,3,3,4] | |
| 4 | 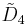 |
[31,1,1,1] | q[4,3,3,4] | |
| 5 | 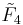 |
[3,4,3,3] | ||
| # | Coxeter group | Coxeter-Dynkin diagram | |
|---|---|---|---|
| 1 | 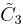 x x |
[4,3,4]x[∞] | |
| 2 | 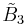 x x |
[4,31,1]x[∞] | |
| 3 | 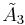 x x |
[3[4]]x[∞] | |
| 4 | 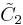 x x x x |
[4,4]x[∞]x[∞] | |
| 5 | 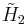 x x x x |
[6,3]x[∞]x[∞] | |
| 6 | 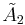 x x x x |
[3[3]]x[∞]x[∞] | |
| 7 |  x x x x x x |
[∞]x[∞]x[∞]x[∞] | |
| 8 | 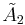 x x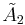 |
[3[3]]x[3[3]] | |
| 9 | 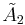 x x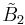 |
[3[3]]x[4,4] | |
| 10 | 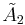 x x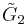 |
[3[3]]x[6,3] | |
| 11 | 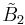 x x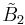 |
[4,4]x[4,4] | |
| 12 | 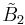 x x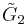 |
[4,4]x[6,3] | |
| 13 | 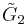 x x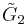 |
[6,3]x[6,3] | |
There are three regular honeycombs of Euclidean 4-space:
- tesseractic honeycomb, with symbols {4,3,3,4}, = . There are 19 uniform honeycombs in this family.
- 24-cell honeycomb, with symbols {3,4,3,3}, . There are 31 reflective uniform honeycombs in this family, and one alternated form.
- Snub 24-cell honeycomb, with symbols h0,1{3,4,3,3}, constructed by four snub 24-cell, one 16-cell, and five 5-cells at each vertex.
- 4-demicube honeycomb, with symbols {3,3,4,3},
Other families that generate uniform honeycombs:
- There are 23 uniform honeycombs, 4 unique in the demitesseractic honeycomb family. With symbols h{4,32,4} it is geometrically identical to the hexadecachoric honeycomb, =
- There are 7 uniform honeycombs from the
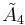 , family, all unique, including:
, family, all unique, including:
- There are 9 uniform honeycombs in the
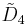 : [31,1,1,1] family, all repeated in other families, including the demitesseractic honeycomb.
: [31,1,1,1] family, all repeated in other families, including the demitesseractic honeycomb.
Non-Wythoffian uniform tessellations in 4-space also exist by elongation (inserting layers), and gyration (rotating layers) from these reflective forms.
Regular tessellations of hyperbolic 4-space
There are five kinds of convex regular honeycombs and four kinds of star-honeycombs in H4 space:[4]
| Honeycomb name | Schläfli Symbol {p,q,r,s} |
Coxeter-Dynkin diagram |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|---|
| Order-5 pentachoric | {3,3,3,5} | {3,3,3} | {3,3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} | |
| Order-3 hecatonicosachoric | {5,3,3,3} | {5,3,3} | {5,3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} | |
| Order-5 tesseractic | {4,3,3,5} | {4,3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3,3,4} | |
| Order-4 hecatonicosachoric | {5,3,3,4} | {5,3,3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3,3,5} | |
| Order-5 hecatonicosachoric | {5,3,3,5} | {5,3,3} | {5,3} | {5} | {5} | {3,5} | {3,3,5} | Self-dual |
There are four regular star-honeycombs in H4 space:
| Honeycomb name | Schläfli Symbol {p,q,r,s} |
Coxeter-Dynkin diagram |
Facet type {p,q,r} |
Cell type {p,q} |
Face type {p} |
Face figure {s} |
Edge figure {r,s} |
Vertex figure {q,r,s} |
Dual |
|---|---|---|---|---|---|---|---|---|---|
| Order-3 stellated hecatonicosachoric | {5/2,5,3,3} | {5/2,5,3} | {5/2,5} | {5} | {5} | {3,3} | {5,3,3} | {3,3,5,5/2} | |
| Order-5/2 hexacosichoric | {3,3,5,5/2} | {3,3,5} | {3,3} | {3} | {5/2} | {5,5/2} | {3,5,5/2} | {5/2,5,3,3} | |
| Order-5 icosahedral hecatonicosachoric | {3,5,5/2,5} | {3,5,5/2} | {3,5} | {3} | {5} | {5/2,5} | {5,5/2,5} | {5,5/2,5,3} | |
| Order-3 great hecatonicosachoric | {5,5/2,5,3} | {5,5/2,5} | {5,5/2} | {5} | {3} | {5,3} | {5/2,5,3} | {3,5,5/2,5} |
Regular and uniform hyperbolic honeycombs
There are 5 compact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in hyperbolic 4-space as permutations of rings of the Coxeter diagrams. There are also 9 noncompact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in 4-space as permutations of rings of the Coxeter diagrams. Noncompact groups generate honeycombs with inifinite facets or vertex figures.
|
|
|
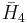 = [3,3,3,5]: = [3,3,3,5]:
|
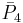 = [3,3[4]]: = [3,3[4]]:
|
|
|
Notes
- ^ A proposed name polyteron (plural: polytera) has been advocated, from the Greek root poly- meaning "many", a shortened tetra- meaning "four", and suffix -on. "Four" refers to the dimension of the 5-polytope facets.
- ^ http://www.steelpillow.com/polyhedra/ditela.html
- ^ George Olshevsky (2006), Uniform Panoploid Tetracombs, manuscript. Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs.
- ^ Coxeter, The Beauty of Geometry: Twelve Essays, Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900 (3 regular and one semiregular 4-polytope)
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973 (p. 297 Fundamental regions for irreducible groups generated by reflections, Spherical and Euclidean)
- H.S.M. Coxeter, The Beauty of Geometry: Twelve Essays (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591] (p. 287 5D Euclidean groups)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Richard Klitzing, 5D, uniform polytopes (polytera)
- James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990) (Page 141, 6.9 List of hyperbolic Coxeter groups, figure 2) [2]
External links
- Polytope names, Guy Inchbald
- Polytopes of Various Dimensions, Jonathan Bowers
- Glossary for hyperspace: Polytope, George Olshevsky
- Multi-dimensional Glossary, Garrett Jones
- polytope names, Wendy Krieger
| Family | An | BCn | Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regular polygon | Triangle | Square | Hexagon | Pentagon | ||||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| n-polytopes | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes | ||||||||||||
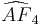 = [(3,3,3,3,4)]:
= [(3,3,3,3,4)]: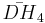 = [5,3,31,1]:
= [5,3,31,1]: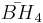 = [4,3,3,5]:
= [4,3,3,5]: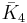 = [5,3,3,5]:
= [5,3,3,5]: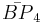 = [4,3[4]]:
= [4,3[4]]: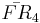 = [(3,3,4,3,4)]:
= [(3,3,4,3,4)]: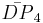 = [3[3]x[ ]]:
= [3[3]x[ ]]: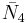 = [4,/3\,3,4]:
= [4,/3\,3,4]: = [3,4,31,1]:
= [3,4,31,1]: = [4,32,1]:
= [4,32,1]: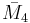 = [4,31,1,1]:
= [4,31,1,1]: = [3,4,3,4]:
= [3,4,3,4]: